Методы анализа, основанные на законах Ома и законах Кирхгофа
Закон Ома устанавливает зависимость между напряжением и током на пассивной ветви, а также позволяет определить ток по известным потенциалам на концах ветви с источником напряжения.
Законы Кирхгофа применяют для нахождения токов в ветвях линейных и нелинейных схем при любом законе изменения во времени токов и напряжений.
Метод эквивалентных преобразований. При эквивалентных преобразований отдельные участки электрической цепи заменяются более простыми. Эквивалентность преобразования состоит в том, что токи и напряжения в непреобразованной части схемы не изменяются.
Последовательное упрощение схемы продолжается до ее преобразования в одноконтурную схему, после чего для расчета используется закон Ома.
Метод эквивалентных преобразований используется для нахождения внутреннего сопротивления эквивалентного генератора.
При помощи метода эквивалентных преобразований облегчают расчет расчет нелинейной цепи, упростив линейную часть цепи эквивалентными преобразованиями.
Принято пользоваться приведенным ниже алгоритмом метода законов Кирхгофа.
1. Произвольно выбирают положительные направления токов в ветвях и обозначают их на схеме.
2. Составляют уравнения по первому закону Кирхгофа: на одно уравнение меньше числа узлов (для последнего узла уравнение будет зависимым от предыдущих уравнений).
3. Выбирают независимые (главные) контуры и направление их обхода. Удобно для всех контуров выбрать одинаковое направление обхода.
4. Записывают уравнения по второму закону Кирхгофа для выбранных контуров.
5. Решая полученную систему уравнений, определяют искомые токи.
Задача 1.1. Определить эквивалентное сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К методом эквивалентных преобразований (рис. 1.1, a).
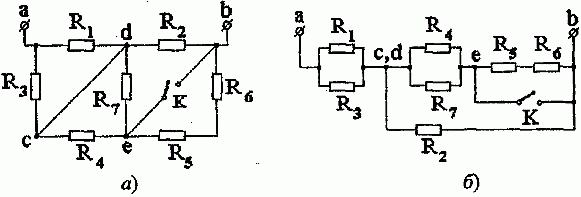
Рис. 1.1
Решение. Сохраняя топологию схемы, трансформируем ее к виду, удобному для анализа (отправная точка – потенциалы узлов c и d равны между собой).
Из рис. 1.1, б следует:
1. При разомкнутом ключе К
2. При замкнутом ключе К
где
Задача 1.2. Определить методом эквивалентных преобразований сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К для схемы, изображенной на рис. 1.2.

Рис. 1.2
Решение. Совершим поворот части схемы относительно зажимов c и d. В результате получим (рис. 1.3):
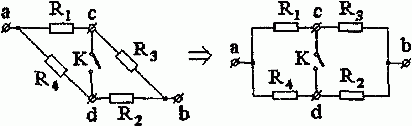
Рис. 1.3
1. При разомкнутом ключе К
2. При замкнутом ключе К
Задача 1.3. Найти сопротивление между зажимами a и b для схемы, изображенной на рис. 1.4.

Рис. 1.4
Решение. К точке 2 подходят условные «начало» сопротивления R2 и «концы» сопротивлений Rlи R3.
К точке 3 подходят «начала» сопротивлений R1 и R3 и «конец» сопротивления R2.
Но тогда, все «начала» сопротивлений и все их «концы» соединяются соответственно в одни точки. А значит, по определению, имеем параллельное соединение приемников (рис. 1.5).
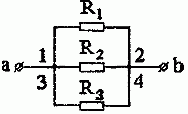
Рис. 1.5
Таким образом, сопротивление между зажимами a и b:
Задача 1.4. Найти сопротивление R13, R14, R17 между различными парами вершин куба, ребра которого имеют заданное сопротивление R (рис. 1.6).
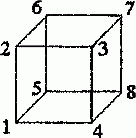
Рис. 1.6
Решение. Задачу проще всего решить методом амперметра и вольтметра. Суть метода заключается в следующем. Если к фиксированным точкам схемы a и b подвести условно известное напряжение Uab и определить ток I во внешней цепи, то искомое сопротивление Rab = Uab/I. При этом напряжение Uab (показание вольтметра) в соответствии с законами Кирхгофаопределяется как функция тока I (показание амперметра).
1. Расчетная схема для определения сопротивления R13 имеет вид, представленный на рис. 1.7.
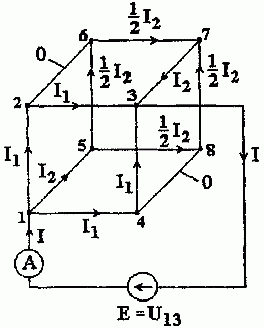
Рис. 1.7
В силу симметрии потенциалы точек 2 и 6 (4 и 8) равны между собой. Поэтому токи в ребрах. 2 – 6 и 4 – 8 отсутствуют.
Перераспределение токов I1 и I2 легко находится из первого закона Кирхгофа и соответствует рисунку 1.7.
Соотношение между токами найдем из второго закона Кирхгофа:
Откуда:
А значит, общий ток
Но
Откуда, сокращая на I1, имеем 8/3·R13 = 2R. Или, что-то же, искомое R13 = 3/4·R.
2. Расчетная схема для определения сопротивления R14 имеет вид, представленный на рис. 1.8.
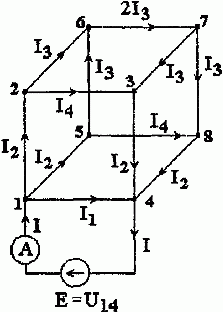
Рис. 1.8
В силу симметрии токи в ребрах 1 – 2, 1 – 4, 2 – 3 и 4 – 3 равны между собой. А значит, в соответствии с первым законом Кирхгофа, токи в ребрах 2 – 6 и 4 – 8 отсутствуют.
Перераспределение неизвестных токов I1, I2, I3, I4 находится из первого закона Кирхгофа (и симметрии цепи) и соответствует рис. 1.8.
Поскольку падение напряжения
то, сокращая на R, имеем:
или
Ток
или
Но
Откуда, сокращая на R, имеем:
или
Но
Или, что то же, искомое R14 = 14/24·R = 7/12·R.
3. Расчетная схема для определения сопротивления R17 имеет вид, представленный на рис. 1.9.
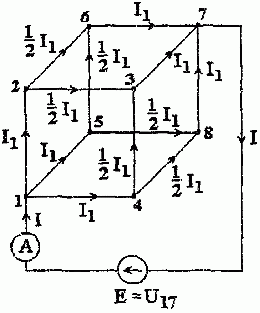
Рис. 1.9
В силу диагональной симметрии схемы полный ток I = 3I1.
Падение напряжения
Откуда искомое сопротивление R17 = 5/6·R.
Задача 1.5. Определить методом эквивалентных преобразований токи в ветвях цепи (рис. 1 10,а) и показание вольтметра, включенного между точками c и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи.
Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю?
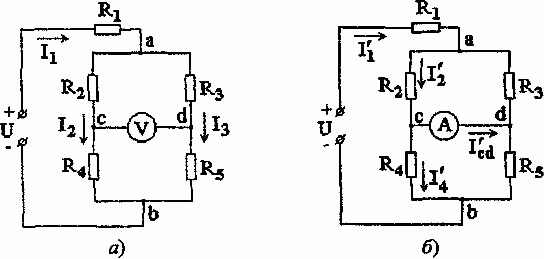
Рис. 1.10
Сопротивления элементов цепи: R1 =10 Ом, R2 = R3 = R5 = 25 Ом и R4 = 50 Ом, а приложенное к ней напряжение U = 120 В.
Решение. Расчет показания вольтметра. Из условия вытекает, что его включение не оказывает влияния на распределение токов в цепи. Для расчета токов сначала определяем эквивалентное сопротивление всей цепи (рис. 1.10, а):
В неразветвленной части цепи протекает ток
Токи, протекающие через сопротивления (R2 + R4) и (R3 + R5) можно найти различными способами.
1. В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формула разброса токов):
2. Найдем напряжение на зажимах параллельных ветвей:
Токи в ветвях с сопротивлениями R2 + R4 и R3 + R5 равны:
Напряжение на зажимах параллельных ветвей может быть найдено как разность между приложенным напряжением и падением напряжения на сопротивлении R1: Uab = U – R1·I1.
Найдем показание вольтметра, равное напряжению между точками с и d:
Наконец, вычислим ток, проходящий через амперметр; он равен току короткого замыкания I’cd (рис. 1.10, б). Для его нахождения вычислим токи:
Искомый ток, проходящий через амперметр,
Задача 1.6. В схеме рис. 1.11 заданы сопротивления приемников, величины ЭДС и источника тока отдельных ветвей. Рассчитать неизвестные токи, ЭДС E2 и сопротивление R5, пользуясь законами Кирхгофа.
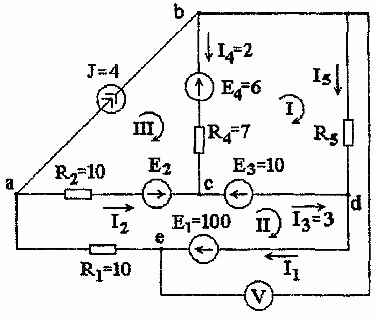
Рис. 1.11
Правильность решения проверить по балансу мощностей. Для наружного контура построить потенциальную диаграмму и определить показание вольтметра.
Решение
1. Всего в схеме пять ветвей, неизвестных токов I1, I2, I5 – три, неизвестных величин E2 и R5 – две, для нахождения которых составам три уравнения по первому закону Кирхгофа и два – по второму закону Кирхгофа:
Из первых трех уравнений находим токи:
из четвертого уравнения
Величину E2 определяем из последнего уравнения:
2. Для построения потенциальной диаграммы найдем потенциалы всех точек контура abcdea, приняв исходный потенциал точки a равным нулю:
3. По найденным потенциалам строим потенциальную диаграмму, откладывая по оси ординат потенциалы точек, а по оси абсцисс – сопротивления участков (рис. 1.12).
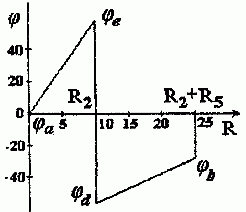
Рис. 1.12
3. Из потенциальной диаграммы легко определить разность потенциалов между точками b и c Ubc = 70 В, что и будет показывать вольтметр.
4. Произведем проверку баланса мощностей:
В этом уравнении нам неизвестно напряжение на зажимах источника тока Uba, которое легко найти из потенциальной диаграммы: Uba = –20 В. С учетом этого


Поделиться с друзьями: