e-mail:cayann@yandex.ru

Херсон , ул. 40 лет Октября, 23

Херсонский политехнический колледж ОНПУ

Заголовок

Решение задач на Метод узловых потенциалов

В методе узловых потенциалов за вспомогательные расчетные величины принимают потенциалы узлов схемы. При этом потенциалом одного из узлов задаются, обычно считая его равным нулю (заземляют). Этот узел называют опорным узлом. Затем для каждого узла схемы, кроме опорного узла, составляют систему уравнений методом узловых потенциалов. По найденным потенциалам узлов находят токи ветвей по обобщенному закону Ома (закону Ома для ветви с ЭДС).

Отметим, что метод узловых потенциалов без предварительного преобразования схемы не применим к схемам с взаимной индукцией.

Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), не имеющих общего узла нужно применять особые способы составления системы уравнений метода узловых потенциалов.

Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), имеющих общий узел, этот общий узел принимают за опорный узел (заземляют). Тогда потенциалы узлов, соединенных этими идеальными источниками ЭДС без пассивных элементов с опорным узлом, равны ЭДС этих идеальных источников (+E, если идеальный источник ЭДС направлен от опорного узла и –E в противном случае).

Метод двух узлов является частным случаем метода узловых потенциалов. Он применяется для определения токов в ветвях схемы с двумя узлами и произвольным числом параллельных активных и пассивных ветвей.

Решение задач методом узловых потенциалов и методом двух узлов

Задача 1.4.1 Рассчитать цепь рис. 1.4.1 методом узловых, потенциалов.

Задача 1.4.1 Рассчитать цепь рис. 1.4.1 методом узловых, потенциалов

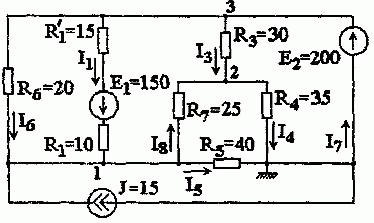
Рис. 1.4.1

Решение. В рассматриваемой схеме четыре узла. Заземлим узел 4 (опорный узел)

φ 4 = 0.

Тогда

φ 3 = φ 4 + E 2 = 200 B .

Необходимо найти потенциалы узлов 1 и 2. Составим систему уравнений по методу узловых потенциалов для узлов 1 и 2.

Рассматривая узел 1, получим

φ 1 \cdot g 11 - φ 2 \cdot g 12 - φ 3 \cdot g 13 = J + E 1 R 1 + R ' 1

или

φ 1 \cdot g 11 - φ 2 \cdot g 12 = J + E 1 R 1 + R ' 1 + E 1 \cdot g 13 .

В правой части этого уравнения оба слагаемых учтены со знаком плюс, так как J и E₁ направлены к узлу 1.

Рассматривая узел 2 (правая часть уравнения равна нулю, так как в ветвях, подсоединенных к узлу 2, нет источников энергии), получим

- φ 1 \cdot g 21 + φ 2 \cdot g 22 - φ 3 \cdot g 23 = 0

или

- φ 1 \cdot g 21 + φ 2 \cdot g 22 = E 2 \cdot g 23 .

Найдем собственную проводимость первого узла

g 11 = 1 R 6 + 1 R 1 + R ' 1 + 1 R И Т + 1 R 2 + 1 R 5 = 1 20 + 1 25 + 1 25 + 1 40 = 0,155 С м .

Проводимость ветви с идеальным источником тока равна нулю, так как внутреннее сопротивление идеального источника тока R_ИТ равно бесконечности.

Собственная проводимость узла 2

g 22 = 1 R 2 + 1 R 3 + 1 R 4 = 1 25 + 1 30 + 1 35 = 0,102 С м .

Взаимные проводимости между узлами

g 13 = 1 R 6 + 1 R 1 + R ' 1 = 1 20 + 1 25 = 0,09 С м; g 21 = g 12 = 1 R 2 = 1 25 = 0,04 С м; g 23 = 1 R 3 = 1 30 = 0,033 С м .

Подставив в уравнения известные величины, получим

{φ 1 \cdot 0,155 - φ 2 \cdot 0,04 = 39 - φ 1 \cdot 0,04 + φ 2 \cdot 0,102 = 6,6

Для решения этой системы используем метод определителей. Главный определитель системы

Δ = ∣ ∣ ∣ 0,155 - 0,04 - 0,04 0,102 ∣ ∣ ∣ = 0,01421.

Частные определители

Δ 1 = ∣ ∣ ∣ 39 6,6 - 0,04 0,102 ∣ ∣ ∣ = 4,242; Δ 2 = ∣ ∣ ∣ 0,155 - 0,04 39 6,6 ∣ ∣ ∣ = 2,583.

Находим потенциалы узлов

φ 1 = Δ 1 Δ = 4,242 0,01421 = 298,6 В; φ 2 = Δ 2 Δ = 2,583 0,01421 = 181,8 В .

Определяем токи в ветвях (положительные направления токов в ветвях с ЭДС выбираем по направлению ЭДС, в остальных ветвях произвольно)

I 1 = φ 3 - φ 1 + E 1 R 1 + R ' 1 = 200 - 298,6 + 150 10 + 15 = 2,056 А .

В числителе этого выражения от потенциала узла 3, из которого вытекает ток I₁, вычитается потенциал узла 1, к которому ток подтекает. Если ЭДС ветви совпадает (не совпадает) с выбранным направлением тока, то она учитывается со знаком плюс (минус). В знаменателе выражения учитываются сопротивления ветви.

Аналогично определяем другие токи (направления токов указаны на схеме рис. 1.4.1)

I 1 = φ 3 - φ 1 R 6 = 200 - 298,6 20 = - 4,93 А; I 2 = φ 1 - φ 2 R 2 = 298,6 - 181,8 25 = 4,67 А; I 3 = φ 3 - φ 2 R 3 = 200 - 181,8 30 = 0,607 А; I 4 = φ 2 - φ 4 R 4 = 181,8 - 0 35 = 5,194 А .

Для определения тока в ветви с идеальной ЭДС зададимся направлением тока I₇. По первому закону Кирхгофа для узла 3 составим уравнение

- I 7 + I 3 + I 1 + I 6 = 0.

Откуда

I 7 = I 3 + I 1 + I 6 = 0,607 + 2,056 - 4,98 = - 2,317 A .

Задача 1.4.2 Определить токи в схеме рис. 1.4.2 методом узлового напряжения.

Задача 1.4.2 Определить токи в схеме рис. 1.4.2 методом узлового напряжения

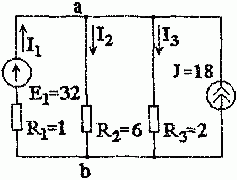
Рис. 1.4.2

Решение

1 Находим напряжение между двумя узлами по методу двух узлов

U a b = φ a - φ b = E 1 \cdot g 1 + J g 1 + g 2 + g 3 = 32 \cdot 1 1 + 18 1 1 + 1 6 + 1 2 = 30 B .

При составлении этого уравнения по методу двух узлов в числителе необходимо брать произведение ЭДС на проводимость своей ветви со знаком плюс, если ЭДС направлена к узлу a, и минус – если направлена от узла a к узлу b.

Аналогичное правило определяет и знаки токов источников тока.

2 Находим токи по закону Ома (по закону Ома для ветви с ЭДС)

I 1 = E 1 + φ b - φ a R 1 = E 1 - U a b R 1 = 32 - 30 1 = 2 А; I 2 = U a b R 2 = 30 6 = 5 А; I 3 = U a b R 3 = 30 2 = 15 А .

Правильность решения проверим по первому закону Кирхгофа

I 1 - I 2 + I 3 + J = 0; 2 - 5 - 15 + 18 = 0.