Решение задач на Метод наложения

          Метод наложения основан на свойстве линейности электрических цепей. Метод наложениясправедлив только для линейных цепей. Метод наложения применяется для определения токов в ветвях схемы с несколькими источниками.

      Алгоритм метода наложения:

1) выбирают положительные направления токов в ветвях цепи;

2) находят частичные токи в ветвях, вызванные каждым источником по отдельности (схему рассчитывают столько раз, сколько источников действует в схеме);

3) токи в ветвях по методу наложения находят как алгебраическую сумму частичных токов (знакчастичного тока при суммировании определяется по положительному направлению тока ветви).

Решение задач методом наложения

Задача 1.2.1. В электрической цепи рис. 1.2.1 с тремя источниками энергии определить все токи в ветвях, воспользовавшись методом наложения.

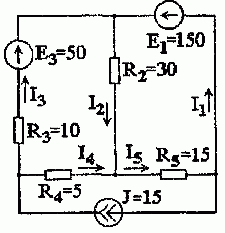
Рис. 1.2.1

Решение

1. Выполним расчет цепи при воздействии источника ЭДС E₁, полагая E₃ = 0, J = 0. Источники считаем идеальными, поэтому внутренние сопротивления ЭДС равны нулю, а источника тока – бесконечности. С учетом этого изобразим расчетную схему (рис. 1.2.2).

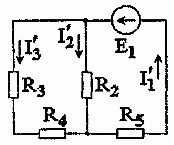
Рис. 1.2.2

Определение токов в полученной схеме будем вести, пользуясь методом эквивалентных преобразований:

2. Расчет электрической цепи при воздействии ЭДС источника Е₃ выполним, полагая Е₁ = 0, J = 0 (рис. 1.2.3).

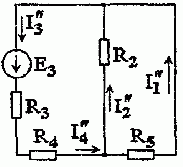
Рис. 1.2.3

В соответствии с рис. 1.2.3 имеем:

3. Расчет электрической цепи при действии источника тока выполним, полагая E₁ = 0, Е₂ = 0 (рис. 12.4).

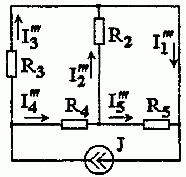
Рис. 1.2.4

В соответствии с рис. 1.2.4 имеем:

Находим токи в параллельных ветвях:

Ток I?I? рассчитываем по первому закону Кирхгофа:

4. В соответствии с принятыми направлениями токов в исходной схеме определим их значения по методу наложения как алгебраическую сумму частичных токов всех промежуточных расчетных схем:

Правильность решения задачи проверяем по первому закону Кирхгофа:

Токи I₁ и I₂ получились отрицательными, т.е. их истинное направление в схеме противоположно принятому положительному направлению.