Решение задач на Метод контурных токов

В методе контурных токов за основные неизвестные величины принимают контурные токи, которые замыкаются только по независимым контурам (главным контурам). Контурные токи находят, решая систему уравнений, составленную по второму закону Кирхгофа для каждого контура. По найденным контурным токам определяют токи ветвей схемы.

Алгоритмом метода контурных токов:

1. Задаются направлением токов ветвей и обозначают их на схеме.

2. Определяют независимые контуры и их нумеруют. При наличии в схеме источников токанезависимые контуры, для которых составляются уравнения метода контурных токов, можно определить, если мысленно удалить источники тока.

3. Выбирают направление контурных токов (целесообразно в одну сторону) и составляют уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока. Контурный ток, проходящий через источник тока, известен и равен току источника тока (через источник тока проходит только один контурный ток!).

4. Полученную систему алгебраических уравнений решают относительно неизвестных контурных токов.

5. Искомые токи по методу контурных токов находят как алгебраическую сумму контурных токов, проходящих по данной ветви. Токи в ветвях связи равны контурным токам.

Решение задач методом контурных токов

Задача 1.3.1. Определить токи в ветвях схемы рис. 1.3.1 методом контурных токов. Правильность решения проверить по балансу мощностей.

Задача 1.3.1. Определить токи в ветвях схемы методом контурных токов. Правильность решения проверить по балансу мощностей

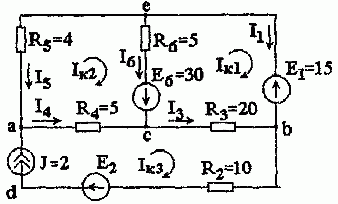
Рис. 1.3.1

Решение

1. В соответствии с алгоритмом, зададимся направлением токов ветвей и обозначим их на схеме рис. 1.3.1.

2. Определяем независимые контура и выбираем направления контурных токов I_к₁, I_к₂, I_к₃.

3. Поскольку в схеме имеется ветвь, содержащая источник тока J, контурный ток I_к₃ = J, а для контурных токов I_к₁ и I_к₂ запишем систему уравнений метода контурных токов:

{I к 1 \cdot (R 3 + R 6) - I к 2 \cdot R 6 - J \cdot R 3 = - E 1 - E 6 I к 2 \cdot (R 4 + R 5 + R 6) - I к 1 \cdot R 6 - J \cdot R 4 = E 6

или

{I к 1 \cdot (R 3 + R 6) - I к 2 \cdot R 6 = - E 1 - E 6 + J \cdot R 3 - I к 1 \cdot R 6 + I к 2 \cdot (R 4 + R 5 + R 6) = E 6 + J \cdot R 4

Подставив значения сопротивлений, получаем численную систему уравнений метода контурных токов с двумя неизвестными контурными токами:

{25 I к 1 - 5 I к 2 = - 5 - 5 I к 1 + 14 I к 2 = 40

откуда

I к 1 = 0,4 A; I к 2 = 3 A .

4. Определяем токи в ветвях схемы по методу контурных токов:

I 1 = I к 1 = 0,4 A; I 5 = - I к 2 = - 3 A; I 6 = I к 2 - I к 1 = 3 - 0,4 = 2,6 A .

Хотя все токи в ветвях можно определить методом контурных токов (I₃ = I_к₃ – I_к₁; I₄ = I_к₃ – I_к₂), токи I₃ и I₄ определим по первому закону Кирхгофа. Составим уравнения по первому закону Кирхгофа:

для узла a:

- I 5 - J + I 4 = 0,

откуда

I 4 = I 5 + J = (- 3) + 2 = - 1 A;

для узла b:

- I 1 - I 3 + J = 0,

откуда

I 3 = J - I 1 = 2 - 0,4 = 1,6 A .

5. Правильность решения проверяем по балансу мощностей. Предварительно находим напряжение на зажимах источника тока:

U a d = φ a - φ d = J \cdot R 2 + I 3 \cdot R 3 + I 4 \cdot R 4 - E 2 = = 2 \cdot 10 + 1,6 \cdot 20 + (- 1) \cdot 5 - 10 = 37 B .

Тогда

E 2 \cdot J + U a d \cdot J + E 1 \cdot (- I 1) + E 6 \cdot I 6 = J 2 \cdot R 2 + I 23 \cdot R 3 + I 24 \cdot R 4 + I 25 \cdot R 5 + I 26 \cdot R 6; 10 \cdot 2 + 37 \cdot 2 + 15 \cdot (- 0,4) + 30 \cdot 2,6 = 22 \cdot 10 + 1,6 2 \cdot 20 + (- 1) 2 \cdot 5 + (- 3) 2 \cdot 4 + 2,6 2 \cdot 5; 166 В т = 166 В т .