Фрагменты эл. цепи называются эквивалентными, если при замене одного из них другим состояние остальной части цепи не изменяется.
Замена фрагментов цепи эквивалентными применяется в основном для упрощения расчетов и схем эл. цепей.
Рассмотрим часто встречающиеся эквивалентные фрагменты эл цепей.
Доказательство эквивалентности основано на законах Кирхгофа и уравнениях элементов эл. цепей.
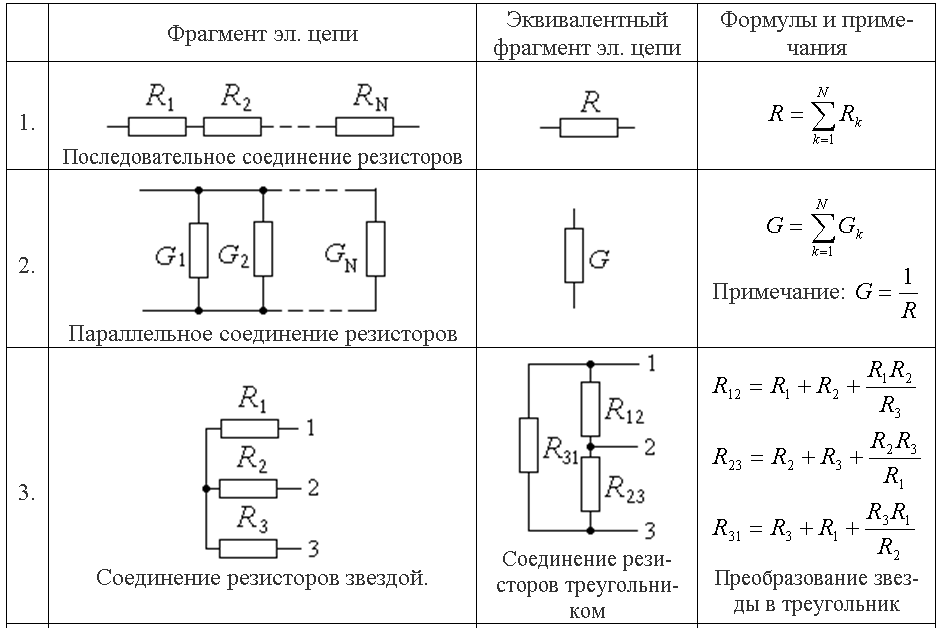

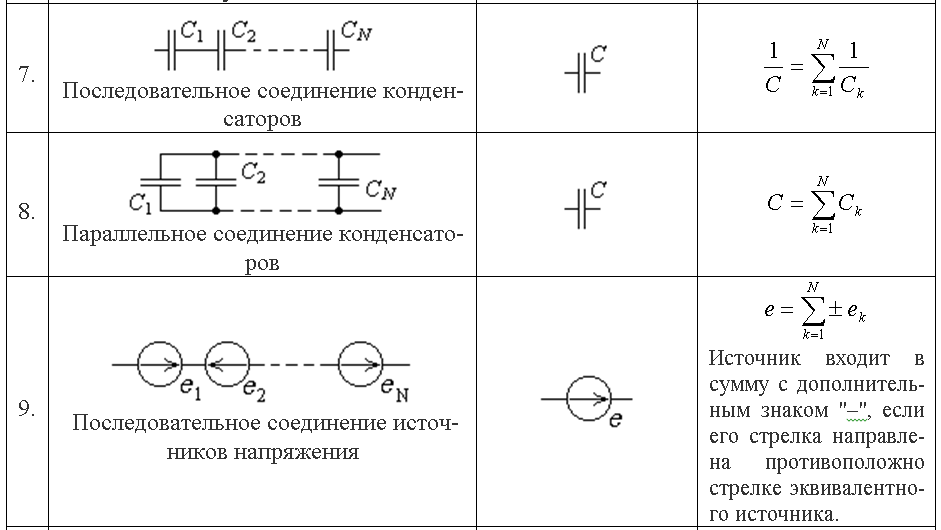
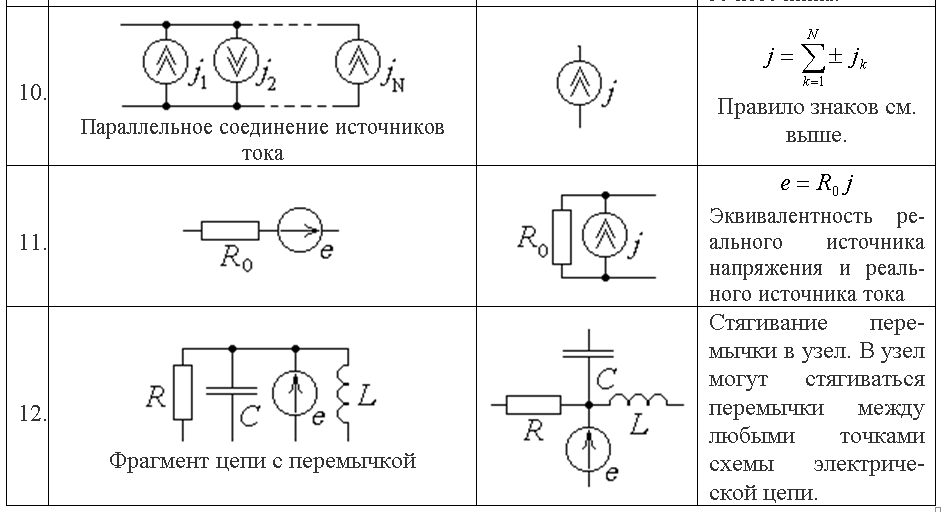
Эквивалентное преобразование треугольника и звезды сопротивлений
Пусть требуется рассчитать цепь, показанную на рис. 1, а.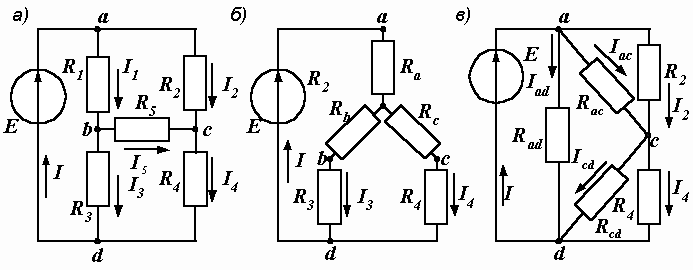
Рис. 1. Преобразования электрической цепи
Расчет можно осуществить одним из известных методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.
Треугольник и звезда сопротивлений имеют вид, показанный на рис. 1.13.
Рис. 1.13. Треугольник и звезда сопротивлений
Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.
Можно показать, что условием эквивалентности являются следующие уравнения:
а) при преобразовании треугольника в звезду: ; ;
; ;
 ;
;
б) при преобразовании звезды в треугольник: ;
; 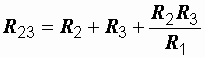 ;
; .
.
Структура приведенных формул проста и легко запоминается.
Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.
При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R3.
Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В,
R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.
а) Р е ш е н и е п р е о б р а з о в а н и е м т р е у г о л ь н и к а в з в е з д у.
После преобразования треугольника, образованного сопротивлениями R1, R2 и R5, в звезду, получаем схему, показанную на рис. 1.12, б. Обращаем внимание на то, что токи в непреобразованной части схемы (I, I3 и I4) остались теми же.
Сопротивления звезды определяем по сформулированному выше правилу: 6 Ом;
6 Ом;  = 10 Ом;
= 10 Ом; = 15 Ом.
= 15 Ом.
Теперь общее сопротивление цепи легко находится: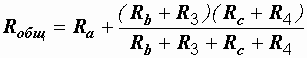 =16,5 Ом.
=16,5 Ом.
Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен 40 А.
40 А.
Токи в параллельных ветвях: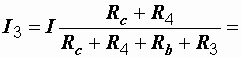 28 A;
28 A;  12 A.
12 A.
Возвращаемся к исходной схеме (рис. 1.12, а): 26 A;
26 A;  14 A.
14 A.
Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A. Знак минус говорит о том, что действительное направление тока I5противоположно указанному на схеме.
б) Р е ш е н и е п р е о б р а з о в а н и е м з в е з д ы в т р е у г о л ь н и к.
Преобразуем звезду, образуемую в схеме на рис. 1.12, асопротивлениями R1, R5и R3,в эквивалентный треугольник (рис. 1.12, в).
Определяем сопротивления треугольника:


Теперь рассчитываем преобразованную цепь.
Сначала находим эквивалентные сопротивления участков ac и cd: ;
; 
Затем определяем общее сопротивление и токи:




Возвращаемся к исходной схеме:![]()
![]()
![]()
Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.


Поделиться с друзьями: